자바스크립트로 이해하는 자료구조 - 복잡도(Complexity)

복잡도 (Complexity)

복잡도(Complexity) 란 알고리즘이나 자료구조가 얼마나 효율적인지 측정하는 기준을 의미합니다.

실행 시간, 메모리 사용량에 따라 크게 시간 복잡도(Time Complexity) 와 공간 복잡도(Space Complexity) 로 나눌 수 있으며 이를 통해 각 알고리즘이나 자료구조의 성능을 객관적으로 비교할 수 있습니다.

시간 복잡도 (Time Complexity)

시간 복잡도(Time Complexity) 란 특정 크기의 입력에 대해 알고리즘이 얼마나 오래 걸리는지 를 의미합니다. 수행 시간은 실행 환경에 따라 다르게 측정되기 때문에 보통 필요한 연산의 횟수로 시간 복잡도를 평가합니다.

시간 복잡도는 일반적으로 최선의 경우, 최악의 경우, 평균의 경우로 나누어 평가됩니다.

• 최선의 경우 (Best Case): 최선의 입력 / 연산 횟수가 가장 적음
• 최악의 경우 (Worst Case): 최악의 입력 / 연산 횟수가 가장 많음

• 평균의 경우 (Average Case): 여러 경우의 수 / 총 연산 횟수를 시행 횟수로 나눈 경우

  보통 알고리즘 분석 시 평균의 경우와 최악의 경우를 가장 많이 분석하며, 알고리즘이 복잡하여 평균을 구하기 어려운 경우 최악의 경우로 알고리즘 성능을 파악합니다.

공간 복잡도 (Space Complexity)

공간 복잡도(Space Complexity) 란 특정 크기의 입력에 대해 알고리즘이 얼마나 많은 메모리를 차지하는지 를 의미합니다.

여기서 공간은 두 가지로 나눌 수 있습니다.

• 고정 공간(Fixed Space): 입력 크기에 상관 없이 항상 일정하게 필요한 메모리 (변수, 상수, 포인터, 인덱스 등 )
• 가변 공간(Variable Space): 입력 크기에 따라 추가로 필요한 메모리 (배열, 객체와 같은 자료구조, 재귀 스택 등)

시간 복잡도와 공간 복잡도는 Trade-off 관계를 가질 수 있습니다. 즉 더 많은 메모리를 사용하여 시간을 절약하거나, 더 많은 시간을 사용하여 메모리를 절약할 수 있습니다.

빅오 표기법 (Big-O notation)

빅오 표기법(Big-O notation) 란 알고리즘의 복잡도를 수학적으로 표현하는 점근 표기법 중 하나 입니다. 다른 표기법으로는 빅오메가(Big-Ω), 빅세타(Big-Θ) 등의 표기법이 있습니다.

왜 빅오 표기법(Big-O notation)을 가장 많이 사용하는가?

빅오 표기법(Big-O notation)이 가장 많이 사용되는 이유는 알고리즘 효율성을 상한선 기준으로 표기하기 때문입니다.

알고리즘 효율성은 값이 클수록, 즉 그래프가 위로 향할수록 비효율적임을 의미하는데 빅오는 상한선을 기준으로 표기하기 때문에 최악의 경우를 고려하는 데 가장 좋은 표기법 입니다.

빅오메가(Big-Ω)는 하한선을 기준으로, 빅세타(Big-Θ)는 상한선과 하한선 사이를 기준으로 표기합니다.

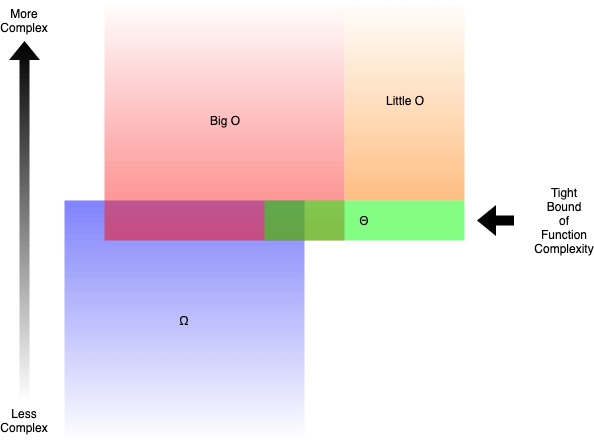Tight Bound of Function Complexity

자바스크립트로 이해하는 빅오 표기법(Big-O notation)

빅오 표기법을 보다 쉽게 이해하기 위해 우선 가장 많이 사용되는 시간 복잡도를 빅오 표기법으로 나타내는 방법을 소개합니다.

O(1) - 상수 시간

function getFirstElement(arr) {
  return arr[0];
}

배열에 인덱스로 접근하는 경우 입력 크기(n)과 상관 없이 항상 한 번에 연산하므로 시간 복잡도는 O(1) 으로 표현할 수 있습니다.

O(n) - 선형 시간

function sumArray(arr) {
  let total = 0;
  
  for (let i = 0; i < arr.length; i++) {
    total += arr[i];
  }
  
  return total;
}

배열에 있는 각 요소의 합을 게산 하기 위해 배열의 크기(n) 만큼의 원소를 순회하므로 시간 복잡도는 O(n)으로 표현 할 수 있습니다.

O(n²) - 이차 시간

function hasDuplicate(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[i] === arr[j]) {
      
        return true;
      }
    }
  }
  
  return false;
}

배열에 있는 중복을 확인하기 위해 배열의 크기(n) 만큼의 원소를 n-1 번 비교하므로 시간 복잡도는 O(n * n) = O(n²)로 표현할 수 있습니다.

O(log n) - 로그 시간

function binarySearch(arr, target) {
  let left = 0;
  let right = arr.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    
    if (arr[mid] === target) {
	    return mid;
    }
     
    if (arr[mid] < target) {
		left = mid + 1;
    } else {
	    right = mid - 1;
    }
  }
  
  return -1;
}

배열에 존재하는 target을 찾기 위해 매 반복마다 배열의 크기(n)를 반씩 줄여가며 찾으므로 시간 복잡도는 n -> n/2 -> n/4로 O(log n)으로 표현할 수 있습니다.

빅오 표기법의 연산 법칙 (Operation Rules In Big O)

위의 간단한 예시를 통해 시간 복잡도를 빅오 표기법(Big-O notation)으로 표현하는 방법을 알아보았습니다.

하지만 빅오 표기법은 단순히 코드에 있는 모든 연산을 더하거나 곱해서 표현하는 것이 아니라 특정한 규칙에 따라 복잡도를 보다 간결하게 표현합니다.

1. 계수 법칙 (Constant Multiple Rule)

상수 배수는 빅오 표기에서 무시됩니다.

(상수 k > 0) f(n)이 O(g(n)) 이면 kf(n)은 O(g(n)) 이다.

function printTwice(arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]); // O(n)
  }
  
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]); // O(n)
  }
}

시간 복잡도는 아래의 합의 법칙에 의해 O(n + n) = O(2n) 으로 계산 되지만 계수 법칙에 의해 상수 배수는 무시되므로 실제 표기는 O(n)으로 표현할 수 있습니다.

2. 합의 법칙 (Sum Rule)

함수가 더해지는 경우 덧셈으로 계산됩니다.

f(n)이 O(h(n)) 이고, g(n)이 O(p(n))이라면 f(n) + g(n)은 O(h(n) + p(n)) 이다.

function process(arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]);  // O(n)
  }
  
  for (let i = 0; i < arr.length ** 2; i++) {
    console.log(i);       // O(n)
  }
}

 시간 복잡도는 합의 법칙에 의해 O(n + n) = O(2n)이지만 계수 법칙이 적용되므로 실제 표기는 O(n)으로 표현할 수 있습니다.

3. 곱의 법칙 (Product Rule)

함수가 중첩되는 경우 곱으로 계산됩니다.

f(n)이 O(h(n)) 이고, g(n)이 O(p(n))이라면 f(n)g(n)은 O(h(n)p(n)) 이다.

function nestedLoop(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr[i], arr[j]);
    }
  }
}

시간 복잡도는 곱의 법칙에 의해 O(n) * O(n) = O(n²) 이므로 실제 표기는 O(n²)으로 표현할 수 있습니다.

4. 다항 법칙 (Polynomial Rule)

다항식에서는 가장 큰 차수만 남깁니다.

f(n)이 k차 다항식이면 f(n)은 O(nᵏ)이다.

function polynomial(arr) {
  let sum = 0;
  
  for (let i = 0; i < arr.length; i++) {      
    for (let j = 0; j < arr.length; j++) {    
      sum += arr[i] * arr[j];
    }
  }
  
  return sum;
}

시간 복잡도는 O(n² + n + 1)이로 계산할 수 있지만 다항 법칙에 의해 가장 큰 차수만 남겨 O(n²)로 표현할 수 있습니다.

빅오 표기법 성능 비교

Big O Complexity Chart

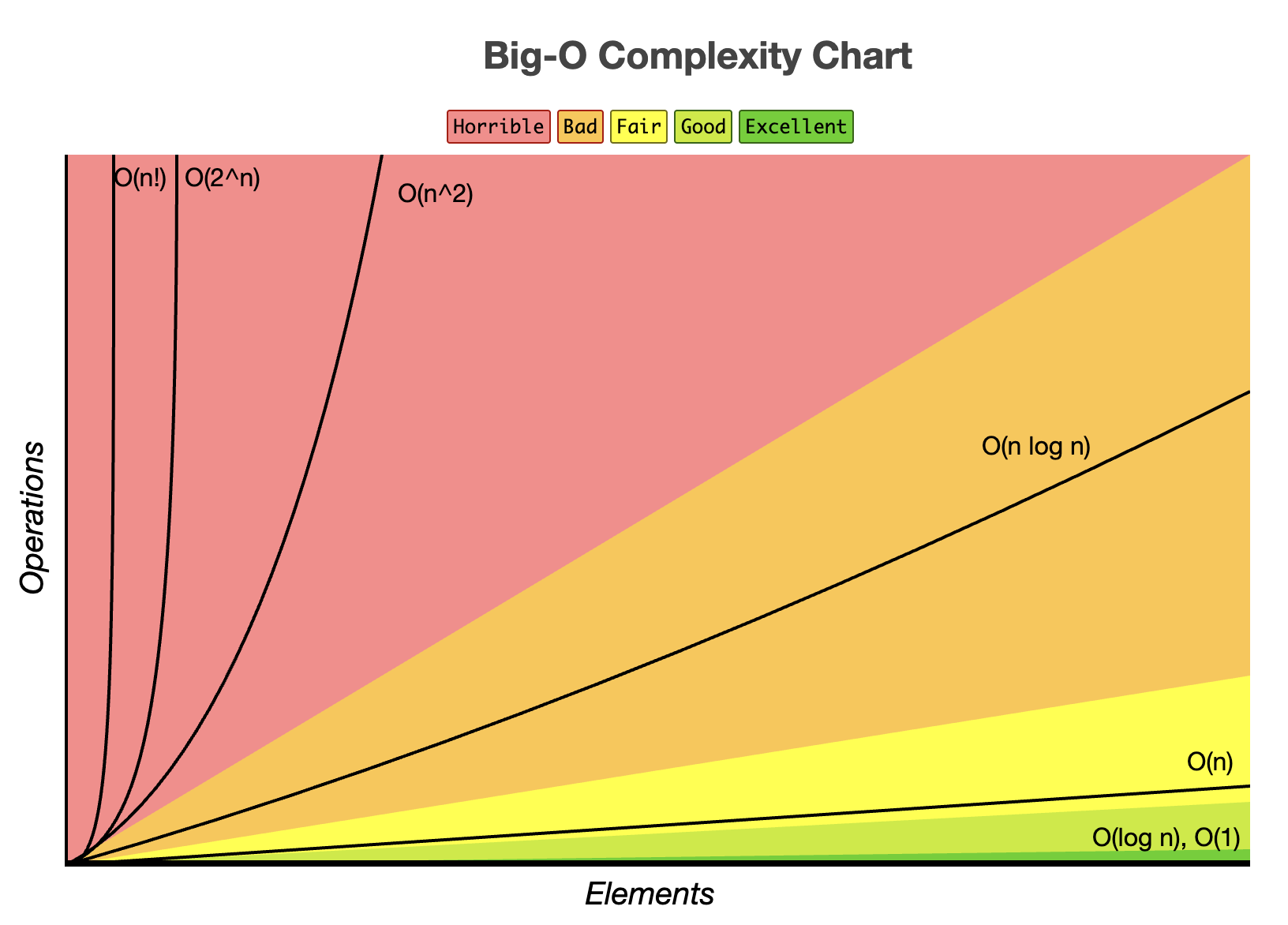
O(1) < O(log n) < O(n) < O(nlog n) < O(n²) < O(2ⁿ)

위의 그래프를 통해 빅오 표기법(Big-O notation)으로 표현된 복잡도의 성능을 한 눈에 비교할 수 있습니다.

이를 통해 우리는 O(1), 상수 시간을 가지는 알고리즘이 가장 성능이 좋고 O(2ⁿ), 지수 시간을 가지는 알고리즘이 성능이 가장 안 좋다는 것을 알 수 있습니다.

빅오 표기법(Big-O notation)의 수학적 정의

빅오 표기법(Big-O notation)의 수학적 정의는 아래와 같습니다.

Big O Defined

모든 N ≥ N₀ 에 대해 f(N) ≤ c * g(N) 을 만족하는 양수인 상수 c와, N₀가 존재한다면 f(N) = O(g(N))을 만족한다.

예를들어 선택 정렬의 수학적 복잡도는 f(n) = n²/2-n/2 와 같은 함수로 표현할 수 있습니다.

이때 g(n)을 n² 이라 정의한다면  c = 1 와 N₀ = 0 일 때 N > N₀ 라는 조건을 만족하는 한, N² 는 N²/2-N/2 보다 항상 큰 값이 된다는 것을 알 수 있습니다.

따라서 f(N) ≤ c * g(N)을 만족하므로 f(n) = O(n²) 으로 표현할 수 있습니다.

빅오 표기법으로 나타낸 자료 구조별 복잡도

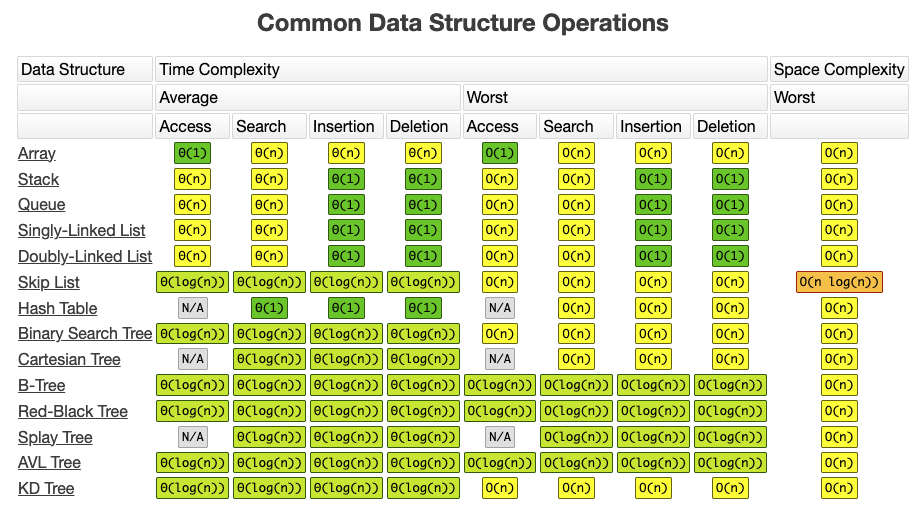Common Data Structure Operations

빅오 표기법으로 나타낸 정렬 알고리즘 복잡도

Array Sorting Algorithms